Tutorial on parametric verification at Petri Nets 2017

Tutorial slides

This page describes the practical session using IMITATOR as part of the tutorial on parametric verification at Petri Nets 2017.

0) Download IMITATOR

The version used for this practical session is IMITATOR 2.9 "Butter Incaberry" (build 2234, Git hash aa3dd87).

The user manual is available there: IMITATOR-user-manual.pdf.

1) Verification of a railway crossing system

Let us consider a railway crossing system with the following specification.

This railway crossing consists in a track crossing a road. Trains can only run in one direction, on a single track. Only one train is present in the system at a time.

A sensor is installed on the tracks, at some distance prior to the railway crossing. The parametric time between the date when the train enables the sensor (action approach) and the date when it reaches the crossing (action pass) is dApproach. When the train enables the sensor, this triggers the start of the gate going down (action startDown). The parametric time between the date when the train enables the sensor and the date when the gate starts to lower is dStartDown. The parametric time between the date when the gate starts lowering and the date when the gate is entirely down (action endDown) is dGetDown.

To keep the system simple, we assume that, if the train has passed when the gate was completely down, then the system restarts in its initial state immediately (i.e., the gate goes back up instantaneously and the train leaves immediately the crossing).

We suppose that cars, bicycles or pedestrians may still cross while the gate is not entirely closed. If the train passes while the gate is not entirely closed, then a collision occurs (technically, may occur), and the system ends in a special location crash.

The goal will of course be to synthesize parameter valuations for dApproach, dStartDown and dGetDown guaranteeing the system safety.

Download and open the file train.imi using your favorite text editor (if you use a KDE environment, Kate with the Ocaml highlighting mode does an almost-perfect job)
Generate a graphical version of the model as follows:
```
> ./imitator train.imi -PTA2JPG
```
This will generate a file train-pta.jpg
Understand the system, and guess what is the role of each location, by rereading the system description above
What is the location that should be unreachable?
Add to the model (below "Property specification") the property that should be verified. The syntax is as follows:
```
property := unreachable loc[system] = SOMETHING;
```
(where SOMETHING should be replaced with the name of the location that shall not be reachable)
Run IMITATOR to automatically synthesize the parameter valuations for which the system is safe:
```
> ./imitator train.imi -mode EF -incl -output-trace-set-verbose
```
IMITATOR will output the result on screen (below "Final constraint such that the system is correct"). What are the parameter valuations guaranteeing the safety of this railway crossing system?
Open the file train-statespace.jpg (that has been automatically generated by the analysis); what is this?

2) Specification and verification of a coffee machine

Let us now write a model for the coffee machine that we saw this morning.

Download and open the skeleton model coffee.imi using your favorite text editor
Enter the following coffee machine model

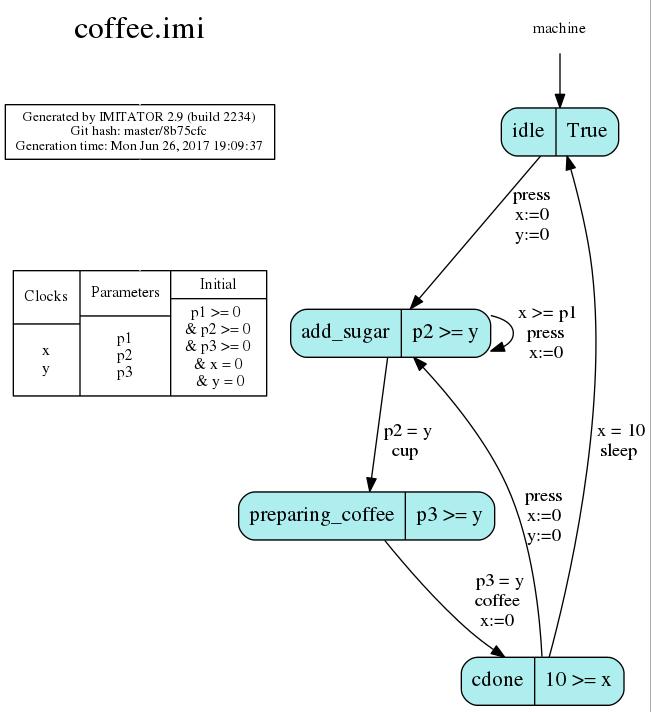
(you may want to reuse the syntax from the previous train.imi file)
You are advised to frequently use the -PTA2JPG command to visualize graphically your automaton and check the syntax.
Using the appropriate command and the appropriate property, synthesize parameter valuations for which it is impossible to get a coffee.
What constraint do you obtain? Can you explain it?
Let us now perform a robustness analysis of this model, using the inverse method [ACEF09]: download the reference valuation file coffee.pi0 using your favorite text editor
What valuation does it define?
Run IMITATOR to automatically synthesize parameter valuations for which the system has the same discrete behavior as in coffee.pi0:
```
> ./imitator coffee.imi coffee.pi0 -mode inversemethod -output-trace-set
```
The result (between "Final constraint such that the system is incorrect" and "This bad constraint is exact (sound and complete)") ensures that, for any parameter valuation satisfying this constraint, the discrete behavior is the same as for the reference valuation. Note that the fact that IMITATOR mentions an "incorrect" constraint is due to the fact that we set the fact that a coffee is delivered as an unsafe state.
You can see a graphical description of the discrete behaviors in the file coffee-statespace.jpg (generated by the analysis). Up to how many sugars can you add to the coffee for these parameter valuations?

3) Additional exercise: A history of noodles

After a long and tiring day working on parametric verification at Petri Nets 2017, a scientist comes back home to cook noodles. S/he puts a pot on a cooking stove at t = 0. After some arbitrary time, s/he starts a timer (action start). The timer will ring pTimer seconds after start (action ring).

At t = pBoilOver, if the timer has not rung yet, the pot boils over (action boilOver). However, if the timer rung before t = pBoilOver, then the pot does not boil over, and noodles are ready! (action ready)

By getting help from the syntax of the previous models, build an IMITATOR input file noodles.imi modeling the noodles problem described above. This PTA will:
- contain at most 2 clocks;
- only contain the actions mentioned in the problem description;
- only contain the two parameters pTimer and pBoilOver;
- only contain guards and invariants in the form x ~ p, where x is a clock, p a parameter, and ~ a comparison operator in {<, <=, = , >= , >}.
What are the parameter valuations guaranteeing that the pot never boils over? Is this result surprising? Please explain.